二叉树的遍历(先序遍历,中序遍历,后序遍历,层次遍历)
二叉树简介
维基百科对二叉树的定义:二叉树(英语:Binary tree)是每个节点最多只有两个分支(不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”和“右子树”。二叉树的分支具有左右次序,不能颠倒。
二叉树的遍历有4种方式,先序遍历,中序遍历,后序遍历,层次遍历,前三者均属于深度优先遍历,先序、中序、后序指的是遍历时根节点相对于左右孩子的次序,先序遍历的顺序为根节点->左子树->右子树,中序遍历的顺序为左子树->根节点->右子树,后序遍历的顺序为左子树->右子树->根节点,遍历时对每个子树采用同样的顺序遍历。层次遍历属于广度优先遍历,顺序为第一层->第二层->第三层->…,每层都按照从左到右的顺序遍历。其中三种深度优先遍历均有递归和非递归两种实现方式。
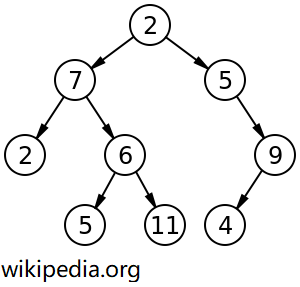
上图四种遍历方式的序列分别为:
- 先序遍历:2, 7, 2, 6, 5, 11, 5, 9, 4
- 中序遍历:2, 7, 5, 6, 11, 2, 5, 4, 9
- 后序遍历:2, 5, 11, 6, 7, 4, 9, 5, 2
- 层次遍历:2, 7, 5, 2, 6, 9, 5, 11, 4
1. 先序遍历
遍历顺序为:根节点->左子树->右子树,分为递归和非递归两种方式
递归算法
思路
先读取根节点的值,然后递归调用遍历函数分别遍历左子树和右子树。
伪代码
PRE_ORDER_RECURSIVE_TRAVERSE(root)
if(root == null)
return
visit(root) //访问根节点
PREORDER_RECURSIVE_TRAVERSE(root.left)
PREORDER_RECURSIVE_TRAVERSE(root.right)
C++实现
void preOrderRecursiveTraversal(TreeNode *root, vector<int> &sequence)
{
if(root == null)
{
return;
}
sequence.push_back(root->val);
preOrderRecursiveTraversal(root->left, sequence);
preOrderRecursiveTraversal(root->right, sequence);
}
非递归算法
思路
使用栈来存储节点,每次打印节点后,右孩子先入栈、左孩子后入栈,这样左孩子就会先出栈,并且打印左孩子时,左孩子的孩子会继续入栈,这样就会先把子树访问完毕,才会出栈右孩子。
伪代码
PRE_ORDER_NONRECURSIVE_TRAVERSE(root)
if(root == null)
return
stack.push(root)
while(stack not empty)
node = stack.pop()
visit(node)
stack.push(node.right) //先入栈右孩子,右孩子会后出栈
stack.push(node.left)
C++实现
vector<int> preOrderTraversal(TreeNode *root)
{
vector<int> sequence;
if(root == nullptr)
{
return sequence;
}
stack<TreeNode *> stackIn;
stackIn.push(root);
while(!stackIn.empty())
{
TreeNode *curNode = stackIn.top();
stackIn.pop();
sequence.push_back(curNode->val);
if(curNode->right)
{
stackIn.push(curNode->right);
}
if(curNode->left)
{
stackIn.push(curNode->left);
}
}
return sequence;
}
2. 中序遍历
遍历顺序为左子树->根节点->右子树,分为递归和非递归两种方式
递归算法
思路
每次递归:先递归遍历左子树,再打印根节点,最后递归遍历右子树
伪代码
IN_ORDER_NONRECURSIVE_TRAVERSE(root)
if(root == null)
return
PREORDER_NONRECURSIVE_TRAVERSE(root.left)
visit(root)
PREORDER_NONRECURSIVE_TRAVERSE(root->right)
C++实现
void inOrderRecursiveTraversal(TreeNode *root, vector<int> &sequence)
{
if(root == nullptr)
{
return;
}
inOrderRecursiveTraversal(root->left, sequence);
sequence.push_back(root->val);
inOrderRecursiveTraversal(root->right, sequence);
}
非递归算法
思路
遍历时,根先入栈,然后一直迭代地访问左孩子,并入栈,直到左孩子为空。此时出栈,打印该节点,该节点的左孩子一定为空(否则前面步骤汇会继续往下走),如果有右孩子,右孩子入栈,进入下次遍历操作。(如果右孩子无左子树,即右孩子的左孩子为空,下次就会打印这个节点,反之会入栈其左子树)
伪代码
IN_ORDER_NONRECURSIVE_TRAVERSE(root)
curNode = root
while(curNode != null && stack is not empty)
while(curNode != null) //先把左孩子都入栈
stack.push(curNode)
curNode = curNode.next
curNode = stack.pop()
visit(curNode)
curNode = curNode->right //左孩子访问完了,访问右孩子
C++实现
vector<int> inOrderTraversal(TreeNode *root)
{
vector<int> sequence;
stack<TreeNode *> stackIn;
TreeNode *curNode = root;
while(curNode || !stackIn.empty())
{
while(curNode)
{
stackIn.push(curNode);
curNode = curNode->left;
}
curNode = stackIn.top();
stackIn.pop();
sequence.push_back(curNode->val);
curNode = curNode->right;
}
return sequence;
}
3. 后序遍历
遍历顺序为左子树->右子树->根节点,分为递归和非递归两种方式
递归算法
思路
先分别递归遍历左子树和右子树,然后打印根节点
伪代码
POST_ORDER_NONRECURSIVE_TRAVERSE(root)
if(root == null)
return
PREORDER_NONRECURSIVE_TRAVERSE(root.left)
PREORDER_NONRECURSIVE_TRAVERSE(root->right)
visit(root)
C++实现
void postOrderRecursiveTraversal(TreeNode *root, vector<int> &sequence)
{
if(root == nullptr)
{
return;
}
postOrderRecursiveTraversal(root->left, sequence);
postOrderRecursiveTraversal(root->right, sequence);
sequence.push_back(root->val);
}
非递归算法
思路
使用栈来存储节点,对每个节点,如果没有左右孩子了,那么打印该节点,如果有孩子,孩子入栈(先右孩子后左孩子,这样左孩子会先出栈)。这种方式面临一个问题,一个节点的左右子树都遍历结束后,会再次访问该节点,这个时候是应该入栈该节点的孩子呢,还是出栈打印该节点呢。无法判断,所以这个时候需要使用一个数据结构(unordered_set)来记录该节点的左右孩子是否已经被访问过了,即入栈了。
伪代码
POST_ORDER_NONRECURSIVE_TRAVERSE(root)
if(root == null)
return
stack.push(root)
while(stack is not empty)
curNode = stack.top()
if(curNode has no child or curNode's child has visited)
visit(curNode)
stack.pop()
else
if(curNode.right != null)
stack.push(curNode.right)
if(curNode.left != null)
stack.push(curNode.left)
visitedNode.add(curNode) //将curNode标记为已访问
C++实现
vector<int> postOrderTraversal(TreeNode *root)
{
vector<int> sequence;
if(!root)
{
return sequence;
}
stack<TreeNode *> stackIn;
stackIn.push(root);
set<TreeNode *> traversed;
while(!stackIn.empty())
{
TreeNode *curNode = stackIn.top();
if(traversed.find(curNode) != traversed.end() || !curNode->left && !curNode->right)
{
sequence.push_back(curNode->val);
stackIn.pop();
continue;
}
if(curNode->right)
{
stackIn.push(curNode->right);
}
if(curNode->left)
{
stackIn.push(curNode->left);
}
traversed.insert(curNode);
}
return sequence;
}
4. 层次遍历
思路
使用队列来按次序保存节点,每次出队列,打印该节点,然后将其左、右孩子分别入栈。
伪代码
LAYER_TRAVERSAL(TreeNode* root)
if(root == null)
return
queue.push(root)
while(queue is not empty)
curNode = queue.pop()
visite(curNode)
if(curNode->left != null)
queue.push(curNode->left)
if(curNode->right != null)
quque.push(curNode->right)
C++实现
vector<int> layerTraversal(TreeNode *root)
{
vector<int> sequence;
if(root == nullptr)
{
return sequence;
}
deque<TreeNode *> que;
que.push_back(root);
while(!que.empty())
{
TreeNode *curNode = que.front();
que.pop_front();
sequence.push_back(curNode->val);
if(curNode->left != nullptr)
{
que.push_back(curNode->left);
}
if(curNode->right != nullptr)
{
que.push_back(curNode->right);
}
}
return sequence;
}